Quadratzahlen

Der Begriff "Quadratzahl" ist durchaus bekannt. Dass diese Zahlen aber genauso heißen, weil sie sich als Quadrat darstellen lassen, ist wiederum manchen nicht bewusst. Sie werden gängigerweise mit Q_n bezeichnet. Im Folgenden sehen Sie die ersten 5 Quadratzahlen und ihre anschaulichen Darstellungen:

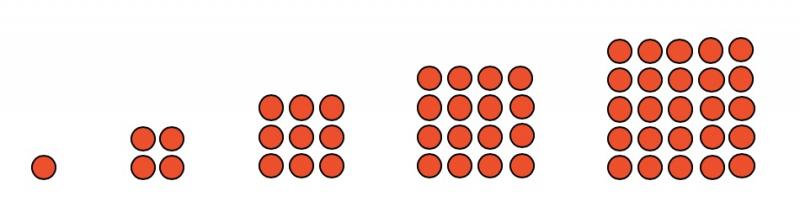
Q₁ = 1 · 1 = 1     Q₂ = 2 · 2 = 4     Q₃ = 3 · 3 = 9         Q₄ = 4 · 4 = 16             Q₅ = 5 · 5 = 25

Die allgemeine Formel für Q_n ist wahrlich nicht schwer zu finden. So gilt für alle natürlichen Zahlen:

Q_n = n · n = n² 

Aber es gibt noch eine "versteckte" Struktur, die auf den ersten Blick nicht sichtbar ist. So gilt gleichermaßen folgender Satz:

Für alle natürlichen Zahlen n ist die Summe der ersten n ungeraden Zahlen gleich der Quadratzahl Q_n . Formal ausgedrückt gilt also folgender Zusammenhang:

1 + 3 + 5 + 7 + ... + (2n-1) =  n · n = n² = Q_n

Dieser Satz wird im folgenden Video anschaulich bewiesen.

 Warum die Summe der ersten n ungeraden Zahlen immer der n-ten Quadratzahl entspricht.

Im folgenden Video wird der Satz:  

1 + 3 + 5 + 7 + ... + (2n-1) =  n · n = n² = Q_n 

anschaulich bewiesen.

Achten Sie vor allem darauf, wie die figurierte Darstellung der ungeraden aufeinanderfolgenden Zahlen strukturiert und zerlegt wird, um den Beweis zu führen. Achten Sie auch darauf, warum der Beweis für gerade n anders verläuft als für ungerade n.