Erklärfilm zur Teilerproduktregel
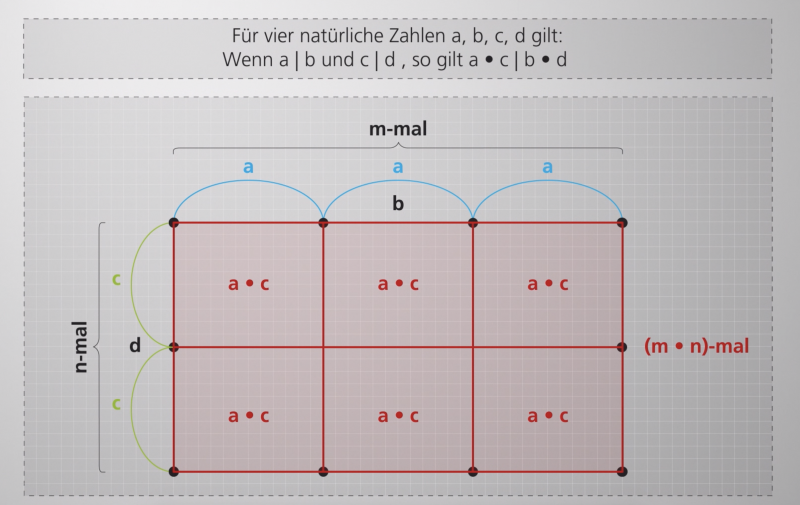
Die Teilerproduktregel besagt, dass für die vier natürlichen Zahlen a, b, c und d gilt:
Wenn a | b und c | d, dann gilt auch a · c | b · d
Anschaulicher Beweis der TEILERProduktregel
Im folgenden Video wird die Teilerproduktregel anschaulich bewiesen. Dabei werden zunächst lineare Darstellungen am Rechenstrich genutzt und zur flächigen aufgespannt. Achten Sie darauf, wie die Idee des Ausmessens zunächst am Rechenstrich und anschließend mit Hilfe von Rechtecken genutzt wird, um den Satz der Teilerproduktregel zu beweisen.
