Lineare diophantische Gleichungen

Eine Gleichung der Form a · x + b · y = c mit ganzzahligen Koeffizienten a, b und c, für die nur ganzzahlige Lösungen für x und y gesucht werden, heißt lineare diophantische Gleichung. 

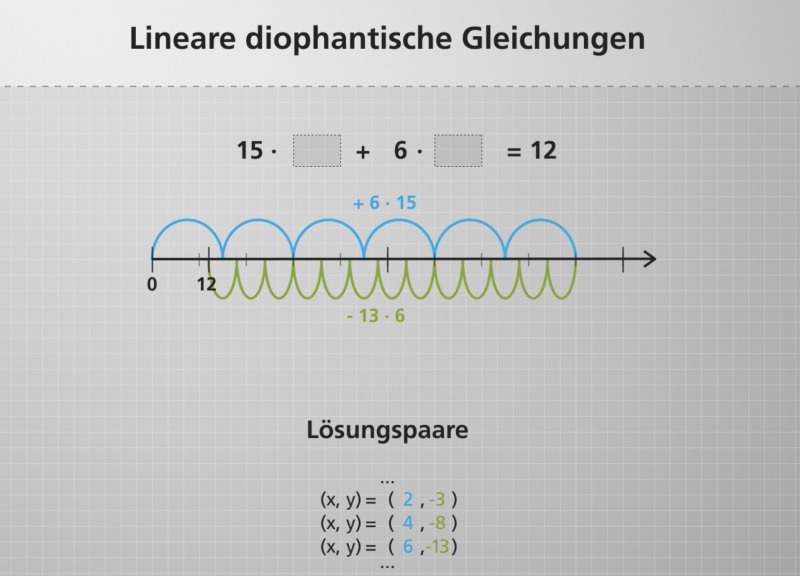
15 · x + 6 · y = 12 ist eine solche lineare diophantische Gleichung. 

Es gibt verschiedene Möglichkeiten, zu einer ersten Lösung der linear diophantischen Gleichung zu kommen. Man kann genau Hinsehen, Vielfachenmengen vergleichen oder den erweiterten euklidischen Algorithmus verwenden. Darum geht es in dem folgenden Video allerdings nicht. Vielmehr geht es darum, ausgehend von einem konkreten Lösungspaar zu verstehen, wie man alle Lösungen der linearen diophantischen Gleichung - also die Lösungsmenge - findet und notiert.

 Aufstellen der Lösungsmenge der linear diophantischen Gleichung

Für die  lineare diophantische Gleichung 15 · x + 6 · y = 12 kann man allein durch genaues Hinsehen schnell das erste Löunsgpaar x = 2 und y = -3 finden. Die Lösungsmenge aller ganzzahligen Lösungen lautet damit: 

L = { x, y ∈ Z |  x =  2 + 2 · k , y = -3 - 5 · k , mit k ∈ Z }

Die Lösungsmenge orientiert sich am kgV von 15 und 6.  Aber warum? Dies wird im folgenden Video illustriert.