Rechteckszahlen

Rechteckszahlen sind Zahlen, die sich mit Hilfe von z. B. Plättchen als Rechteck darstellen lassen, mit der Besonderheit, dass die eine Rechtecksseite um genau 1 größer ist als die andere. Sie werden gängigerweise mit R_n bezeichnet. Im Folgenden sehen Sie die ersten 5 Rechteckszahlen und ihre anschaulichen Darstellungen:

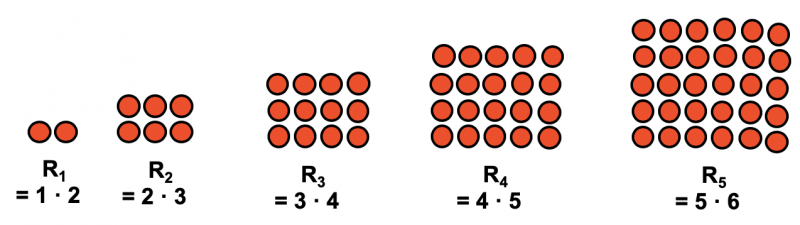
Die explizite Formel für R_n  ist wahrlich nicht schwer zu finden. So gilt für alle natürlichen Zahlen:

R_n = n · (n+1) = n² + n

Aber es gibt noch eine "versteckte" Struktur, die auf den ersten Blick nicht sichtbar ist. So gilt gleichermaßen folgender Satz:

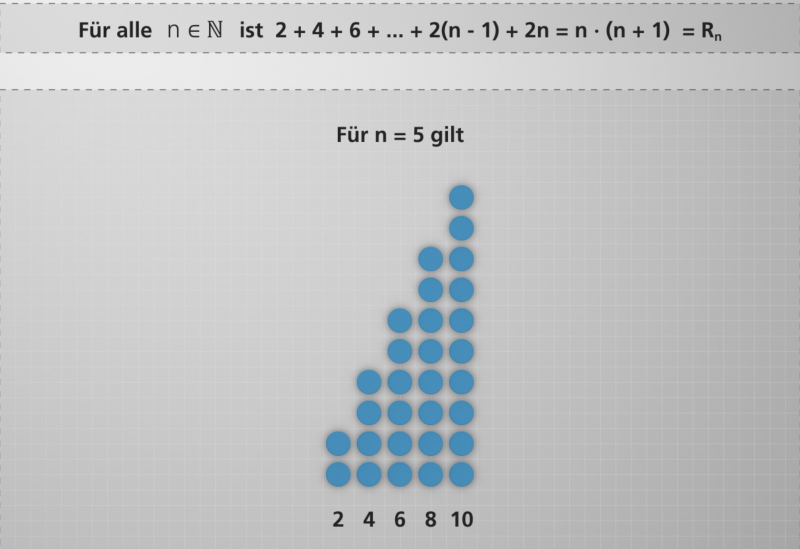
Für alle natürlichen Zahlen n ist die Summe der ersten n geraden Zahlen gleich der Rechteckszahl R_n . Formal ausgedrückt gilt also folgender Zusammenhang:

2 + 4 + 6 + 8 + ... + 2n =  n · (n+1) = n² + n = R_n

Außerdem gibt es einen Zusammenhang zwischen Dreieckszahlen und Rechteckszahlen, der wie folgt lautet:

2 · D_n = R_n

Beide Sätze werden im folgenden Video anschaulich bewiesen.

 Warum die Summe der ersten n geraden Zahlen immer der n-ten Rechteckszahl entspricht.

Im folgenden Video werden folgende Sätze anschaulich bewiesen: Für jede natürliche Zahl n gilt:  

2 + 4 + 6 + 8 + ... + 2n = n · (n+1) = n² + n = R_n     sowie    2 · D_n = R_n

Achten Sie vor allem darauf, wie die figurierten Darstellungen der geraden aufeinanderfolgenden Zahlen strukturiert und zerlegt werden, um den Beweis zu führen. Achten Sie auch darauf, warum der Beweis des ersten Satzes für gerade n anders verläuft als für ungerade n.