Teileranzahl einer Zahl
Die Anzahl aller Teiler einer Zahl kann man über die Primfaktorzerlegung der Zahl bestimmen. In der kanonischen Primfaktorzerlegung werden alle Exponenten um 1 erhöht und miteinander multipliziert. Das Produkt ist gleich der Teileranzahl, z.B.
- 12 = 22 · 31 , hat daher insgesamt (2+1)·(1+1) = 3 · 2 = 6 Teiler
- 25 = 52 , hat daher insgesamt (2+1) = 3 Teiler.
- 30 = 21 · 31 · 51 , hat daher insgesamt (1+1)·(1+1)·(1+1) = 2 · 2 · 2 = 8 Teiler.
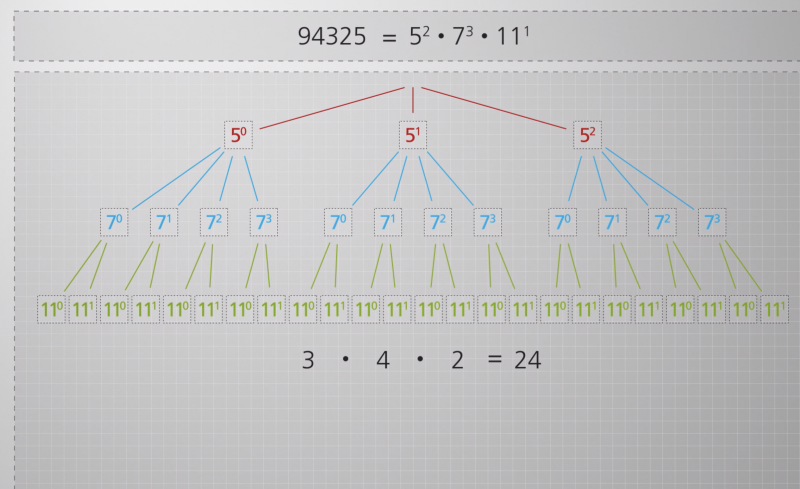
Generischer Beweis der Teileranzahl
Im folgenden Video wird anhand eines generischen Beweises verdeutlicht, warum die Primfaktorzerlegung bei der Bestimmung der Teileranzahl genutzt werden kann. Ebenso wird erläutert, warum alle Exponenten um 1 erhöht werden müssen.
Der Beweis greift auf die Produktregel der Kombinatorik zurück, die Sie sich ggf. ergänzend anschauen sollten.
