Endstellenregel im Dezimalsystem

Die Endstellenregel im Dezimalsystem besagt z. B., dass man bei der Überprüfung der Teilbarkeit durch 4 nur die letzten beiden Stellen der Zahl auf Teilbarkeit durch 4 zu überprüfen braucht. Gleiches gilt für die Teilbarkeit durch 25. So gilt:

4 | 145 624 , denn 4 | 24     und     25 | 2 376 375, denn 25 | 75

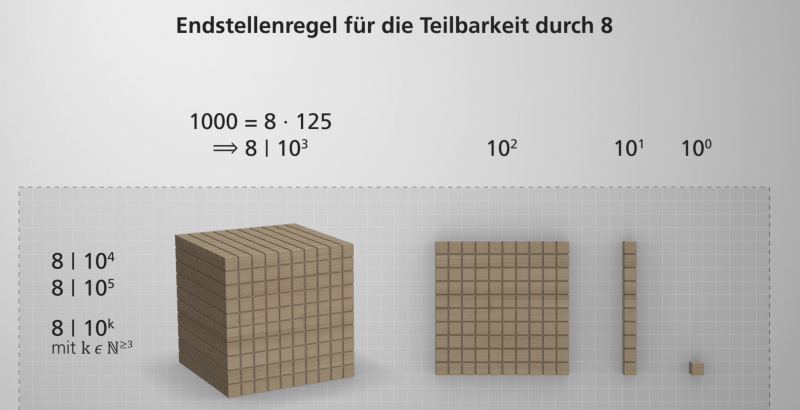
Für die Teilbarkeit durch 8 oder auch durch 125 müssen allerdings die letzten drei Stellen einer Zahl auf Teilbarkeit durch 8 bzw. 125 überprüft werden. 

8 | 145 624 , denn 8 | 624     und     125 | 2 376 375, denn 125 | 375

Aber warum müssen nur genau diese Stellen überprüft werden? Und warum reicht es bei der Überprüfung der Teilbarkeit durch 8 nicht, nur die letzten beiden Stellen zu betrachten? Dies wird im folgenden Video anschaulich illustriert.

 Endstellenregeln im Dezimalsystem

Im folgenden Video wird die Endstellenregel im Dezimalsystem für 4 und 8 generisch bewiesen. Der generische Beweis zeigt sich darin, dass die gewählte Ausgangszahl, die auf Teilbarkeit durch 4 oder 8 überprüft wird, absolut austauschbar ist.