Produktregel der Teilbarkeitsrelation
Eigenaktivität
Man nehme zwei natürliche Zahlen, bei der die eine Zahl ein Teiler der anderen ist, z. B.
3 und 12, denn 3 | 12.
Für jedes Vielfache von 12 gilt nun automatisch, dass auch dieses durch 3 teilbar ist.
3 | 13 · 12 und 3 | 135 · 12 und 3 | 1569 · 12 ... 3 | k · 12 (mit k ∈ ℕ )
Wählen Sie ein eigenes entsprechendes Zahlenpaar, bei dem die kleinere Zahl ein Teiler der größeren ist und überprüfen Sie ebenso, ob Vielfache der größeren Zahl durch die kleinere teilbar sind.
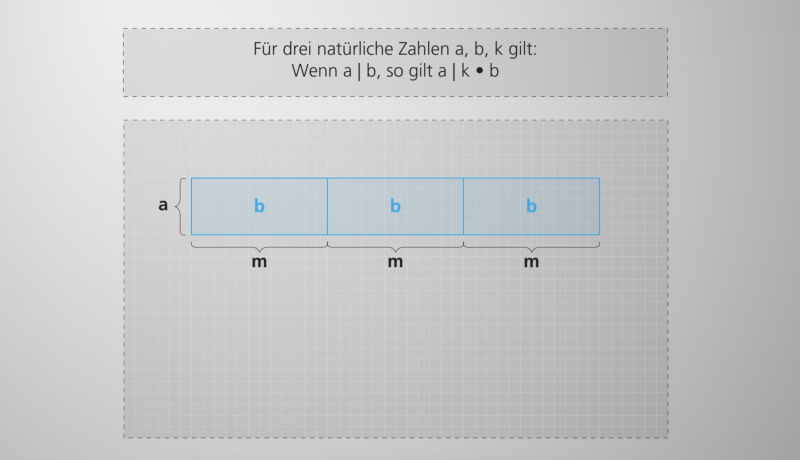
Die Regel, die im obigen Beispiel angewendet wurde, ist die Produktregel der Teilbarkeitsrelation. Sie besagt formal:
Für alle natürlichen Zahlen a, b, k gilt:
Wenn a | b, dann gilt auch a | k · b
Aber warum kann man sich sichern sein, dass diese Regel immer gilt? Diese Aussage gilt es zu beweisen.
Anschaulicher Beweis der Produktregel
Betrachten Sie das folgende Video. In diesem wird die Produktregel anschaulich mit Hilfe von Rechteckfeldern bewiesen.
Achten Sie insbesondere darauf, wie die Voraussetzung a | b mit Hilfe einer Fläche dargestellt wird und wie diese Fläche anschließend vervielfacht wird (also k · b):
